About this site Fundamentals Vectors Matrices Circles and Triangles Complex Numbers Sequences and Series Calculus Appendices Glossary . . .

Advanced mathematics in plain English

You are here: Mathematics → Calculus → Differentiation and Integration

An Introduction to Differentiation and Integration

Imagine you have a mathematical function – any function – which I'll call f.
The value of the function depends on some variable, any variable, which I'll call x. (If your function measures something with respect to time, you might use t instead of x. It doesn't really matter what letters you use for your variables.)

In other words, the value of f (which can also be written as f(x) to reflect its dependence on x) will be different for different values of x.

You can think of a function as a bit like a computer program. It will always output the same answer (the same value) for a particular input (in this case x).

What is a derivative?

If f(x) is the function, then 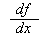is the derivative of that function. Basically, dx represents an infinitesimally small (i.e. really small) change in x, and df represents a corresponding change in f(x) .

In other words: If x changes by a certain amount written as dx, then the value of df  represents exactly how much f(x) will change as a consequence. So if you change x to x + dx, then f will change to f + df.

Actually, the values of df and dx are too small to write down. But if you divide one by the other, then you get the derivative, which is a ratio, 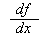, which is equal to the rate of change of f with respect to change in x.

Note that the derivative is not just a simple number - after all, the rate of change of f might not be constant (because only a straight-line graph increases (or decreases) at a constant rate as x increases) - Instead, the derivative is a function, just like f, which depends on x, and gives the instantaneous rate of change of f for any value of x.

x generally represents distance. It doesn't have to be x. It could be a rate of change over time (dt instead of dx). The principle is exactly the same.

What is an integral?

Integration is the opposite of differentiation. When you integrate a function, the resulting function is called an integral. It's a sort of 'running total' that adds up all values so far.

So what happens if you take the integral of a derivative? Well, the derivative gave you a function that showed you the change in your original function at each point. The integral gives you a function that adds up all of those changes at each point, so the function you get back is very similar to your original function (not quite the same, you threw away some information when you took the derivative: how high the function is above the x axis. When you take a derivative and then integrate again, the result will often be off by a constant value).

Another example: What happens if you take the integral of a graph of speed (in metres per second) over time? You get a graph that shows you a running total of distance covered (in metres) at each point in time.

An integral takes a function representing changes, and shows you where those changes lead. A graph of speed is really just a graph of change in distance, for instance. That's why integration is the opposite of differentiation.

---

---